Jan Peter Apel
21.11.2021
7.10.2022 Textstraffung
Ein Desaster
der Wissenschaft
Prolog
Ein
Losspiel mit nur drei Losen, dafür einem showmäßigen Öffnungsritual,
bringt die Wissenschaft seit nun 50 Jahren zur Verzweiflung: Sie
findet keine Erklärung für das zweifelsfrei meßbare Ergebnis und das
läßt sich nur als Blamage der bestehenden Wahrscheinlichkeitslehre
bezeichnen.
Der
Stein des Anstoßes
Im englischen TV gab es in den 70ern des vergangenen Jahrhunderts eine
Unterhaltungsshow, in der ein Auto gewonnen werden konnte, das hinter
einer von drei Türen auf einer TV Tribüne verborgen war. Hinter den
zwei anderen Türen befand sich jeweils eine Ziege. Der Erfinder des
Spiels ließ als
Moderator einen Ratekandidaten eine Tür auswählen, öffnete diese aber
noch nicht. Um der Show einen Clou zu geben, öffnete er statt dessen
mit Worten wie "Ich will Ihnen mal was zeigen"
eine der beiden anderen Türen, von der er wußte, daß sich dahinter eine
Ziege befand. Dann bot er dem Kandidaten auch noch
an, seine Wahl einer Tür noch einmal ändern zu dürfen, also, wenn der
will, die noch übrig gebliebene und geschlossene Tür der beiden anderen
als seine Erstwahl zu deklarieren.
Nach
geraumer Weile zeigte sich, daß, wenn der Ratekandidat seine
Türwahl wechselte, seine Gewinnchance zwei Drittel
betrug.
Die
Alltagswahrscheinlichkeitskenntnisse sagen aber, daß nach Öffnen einer
der drei Türen nur noch zwei Türen übrig sind und damit die
Gewinnwahrscheinlichkeiten der beiden Türen je ein Halb
beträgt. Die tatsächliche Zwei-Drittel-Erfolgsquote wird
aber ungeachtet seiner Wahrheit von einer weltweiten Mehrheit
angezweifelt, da sie von dem "gesunden" Logikempfinden abweicht, man
versteht es nicht oder will es nicht verstehen.
Daraufhin bezeichnete die in den USA mit dem damals höchsten
Intelligenzquotienten
behaftete Frau Marilyn vos Savant die zwei Drittel Gewinnchance beim
Wechseln der Türen als richtig. Ein Shitstorm gegen sie war
die Folge. Frau vos Savant gelang es mit ihrer individuellen
Denkweise aber weder, dieses Ergebnis
sachlich mit Regeln der Wahrscheinlichkeitslehre noch anderweitig
überzeugend zu begründen. Bis heute suchen Mathematik-Koryphäen weiter
nach der Ursache der höheren Gewinnquote, da sie die
Wahrscheinlichkeitslehre als ein Teil der Mathematik betrachten, jedoch
ohne anerkennbare Ergebnisse.
In WIKIPEDIA wird
dieses Problem in äußerst unprofessioneller, unwissenschaftlicher und
unsachlicher Weise vorgestellt. Vor allem verakademisierte sich das
Problem, ohne es als solches erst einmal explizit
zu präzisieren. Statt dessen verbreiterte es sich als diffuses
Problem in ethischer Breite, auch in Büchern, mit zahllosen
diversen Sichtweisen, die bis ins psychische reichen. Dazu werden
Fakten ignoriert sowie Regeln des
Erfinders des Spiels in Frage gestellt und abstruse Gedanken wie z. B.
Verhaltensweisen des Quizmasters mit in Überlegungen einbezogen, als ob
der
Quizmasters das Ergebnis beeinflussen könnte. Mit all dem weiß
niemand mehr, wo vorn und hinten bzw. was überhaupt das eigentliche
Problem ist. Erst
ein bekanntes Problem wird zu einem gelösten Problem.
Das
sachliche Problem heißt:
Warum steigt die Gewinnquote beim Wechsel der Tür durch den
Ratekanditaten auf zwei Drittel?
Die weltweiten Aufregungen entstehen aus dem Problem, daß die
Gewinnsteigerung beim Wechsel der Türen durch den Ratekandidaten
nicht auf 1/2, sondern auf 2/3 steigt, was äußerst unlogisch erscheint
und daher wenig glaubhaft ist. Diese Unglaubhaftigkeit ist
also durch eine sachliche Erklärung zu beenden. Diese Erklärung muß
eindeutig, relativ kurz und für jedermann
nachvollziehbar sein, dazu verständlich und vor allem verbal (keine
mathematischen Formenl!). Alles andere dokumentiert Unwissen des
Erklärers.
Die Regeln des "Ziegen-Spiels" hat der Erfinder Monty
Hall explizit definiert, es ist sein Spiel, er ist der
Erfinder. Mit diesen Regeln muß die
Wahrscheinlichkeitstheorie alle möglichen
Ergebnisse voraussagen.
Die Regeln des Spiels von Monty Hall bestehen aus drei
Schrittabläufen, die er nie variiert hat:
1er
Schritt: Der Ratekandidat wählt eine Tür, die der Moderator
aber noch nicht öffnet.
2er Schritt: Der Moderator öffnet bewußt und absichtlich von seinen
beiden Türen eine, hinter der eine Ziege steht, was er ja weiß.
3er Schritt: Der Moderator gibt dem Ratekandidaten dann die
Möglichkeit, seine Türwahl noch einmal ändern zu dürfen und damit,
wenn er will, zur einzig noch verbleibenden geschlossenen der beiden
anderen Türen zu wechseln.
Diese
und allein diese Abläufe sind von Monty Hall festgelegt und
von ihm in seinen Rateshows immer eingehalten worden. Es ist also
unzulässig zu unterstellen, daß er als Quizmaster z. B. auch
die
vom
Ratekandidaten gewählte Tür öffnen könnte, wenn dahinter eine Ziege
stünde oder er dem Ratekandidaten das Tauschangebot nicht zwingend
machen muß. Mit den drei genannten Schritten ist explizit festgelegt,
was zu tun ist. Damit ist es nicht mehr erforderlich, sagen zu
müssen, was nicht getan werden darf wie z. B. den Tausch nicht
anzubieten. Da
in Schritt 3 bestimmt ist, daß
der Moderator dem Ratekandidaten eine Neuwahl gewährt, heißt das auch
explizit, daß er diese Neuwahl gewähren muß!
Und gerade dieses Tauschangebot ist sogar der Clou
des Spiels, wird in WIKIPEDIA trotzdem als unbestimmt
bewertet. Dummerweise (für die Wissenschaft jedoch
fatalerweise) führt genau diese Wechselmöglichkeit für den Kandidaten
zum Unverständnis über den Fakt, daß das Ergebnis daraus eine Erhöhung
der Gewinnquote auf zwei Drittel ist.
Der
Weg zur Lösung
Rätsel der Natur lösen sich ausschließlich dadurch, daß die
Zusammenhänge deren beteiligter Dinge (beim Ziegenrätsel
"Lose") erkannt werden müssen, so daß daraus Regeln für die
Behandlung der Rätselprobleme entstehen. Diese Regeln sind
wesensbedingt
verbal und niemals mathematisch. Mathematik kann nie
Rätsel lösen, sondern lediglich deren Symptome quantitativ erfassen.
Die Ursache für "Warum sind mathematische Beschreibungen brauchbar?"
bleibt der Mathematik auf ewig verschlossen. Die Lösungen von Rätseln
sind immer verbal und für jeden Interessierten verständlich. Auch für
das Ziegenrätsel muß die Lösung für jedermann leicht
einsichtig sein.
Zur Findung der Lösung gibt es aber ein Problem: eine
sachliche regelgesteuerte Wahrscheinlichkeitslehre gibt es noch
gar nicht! Es gibt einzig mathematische Formulierungen, mit bestimmten
Annahmen auf die Richtigkeit von Ergebnissen hin getrimmt, aber das ist
keine
Wissenschaft.
Was
ist Sache?
Eine Wissenschaft muß zunächst einmal sagen, was für eine
Sache
überhaupt erklärt werden soll. Hier geht es um ein
Losspiel, nur in Form von Türen. Wissenschaftlich
heißt die Gretchenfrage beim Ziegenspiel nach Monty Halls Regen
lediglich, wie ändert sich die Gewinnwahrscheinlichkeit des
Ratekandidaten, wenn
der wechselt. Was hat das mit einem Verhalten des Moderators oder der
Reihenfolge der Öffnungen von Türen (Losen) zu tun? Absolut nichts.
Um Probleme zu lösen, sind diese
zunächst zu analysieren. Dazu ist es hier nötig, das Spiel in die
Terminologie einer sachlichen Wahrscheinlichkeitslehre zu
übersetzen, damit auch eine Allgemeingültigkeit der Lösung entsteht.
Das "Ziegenspiel" entspricht einem Losspiel mit drei Losen, einem
Gewinn
und zwei Nieten. Es gibt zwei Mitspieler, ein Ratekandidat und der
Moderator selbst. Der Ratekandidat wählt ein Los aus, der Moderator
besitzt damit
die zwei anderen.
Eine
Wahrscheinlichkeitslehre muß in der Lage sein,
das Ergebnis eines Losspiels mit nur drei Losen ohne
Mathematik
mit nur ihren eigenen verbalen Prinzipien im Kopf ad hoc vorauszusagen.
Bei Losspielen geht es nicht nur um die Gewinnchancen von Einzellosen,
sondern um die Gewinnchancen von Losbesitzern. Ein
Einzellos hat bei nur einem Gewinnlos immer die
Gewinnchance von 1 durch die Anzahl aller Lose.
Regel 1: Bei Losspielen sind die
Gewinnchancen von Losbesitzern maßgebend.
Ein Losbesitzer mit mehreren Losen
hat die Gewinnchance von einem Los mal der Anzahl seiner Lose.
Für das Ziegenspiel bedeutet
das, daß der Ratekandidat eine Gewinnchance von 1/3 und der Moderator
mit seinen zwei Losen eine von 2/3 haben. Die Konsequenz: bleibt
der Kandidat bei seiner Erstwahl, hat er eine Gewinnschance von
1/3.
Der Quizmaster hat demnach eine Gewinnchance von 2/3, das Auto zu
behalten. Wechselt der Ratekandidat aber zur noch ungeöffneten Tür des
Quizmasters, so zeigt sich als tatsächliches Ergebnis eine
Gewinnchance für ihn von 2/3 und nicht 1/2. Das ist das "Ziegenrätsel",
wobei es das
Problem ist, nicht erklären zu können, warum das Ergebnis 2/3 ist. Da
hilft die folgende Wahrheitstabelle:
Die
Wahrheitstabelle zeigt den Fakt auf, daß der Ratekandidat beim Wechseln
der
Türen eine 2/3 Gewinnchance erhält.
Wahrheitstabellen heißen nicht nur so, sondern zeigen auch die
Wahrheit. Damit ist die Wahrheit beim Ziegenspiel die zwei
Drittel Chance für den Ratekandidaten, wenn der wechselt.
Wahrheitstabellen
sind generell die Grundlagen für die Entstehungen von
Theorien.
Somit wird im Folgenden die Theorie für die Lösung des Ziegenrätsels
erstellt.
Mathematik ist dafür nicht nötig, sie könnte es auch gar nicht.
Die
Findung der Lösung
Was bedeutet eigentlich der Wechsel der Türen für die
Gewinnwahrscheinlichkeit? Der Ratekandidat verläßt seine gewählte
eine Tür und erhält die noch geschlossene des Quizmasters. Der
Quizmaster hatte aber zwei Türen, somit eine 2/3 Gewinnchance.
Der Quizmaster öffnete eine Tür mit Ziege, die er durch seine zwei
Türen ja
immer hat. Der Ratekandidat übernimmt beim Wechsel faktisch aber beide
Türen des Quizmasters. Die geöffnete Tür mit Ziege ist zwar eine Niete,
aber
immer noch ein Los von den dreien und legt damit auch den Nenner der
Gewinnwahrscheinlichkeit mit Drittel fest. Oder anders gesagt:
Beide Türen des Quizmasters stellen die 2/3 Gewinnchance dar. Eine
Niete davon wurde
nur schon vorab "durch Verrat" geöffnet, was die zwei Drittel Chance
des Quizmasters aber nicht mindert. Somit erhält der Ratekandidat immer
noch die volle Gewinnchance des Quizmasters aus zwei Losen, obwohl er
nur noch
eine Tür öffnen kann. Soweit die richtige logische Erklärung, die aber
noch
durch eine sachliche Theorie bestätigt werden muß.
Mehrere Lose eines Losbesitzers
nennen wir nun ein Losbündel. Was es mit Losbündeln
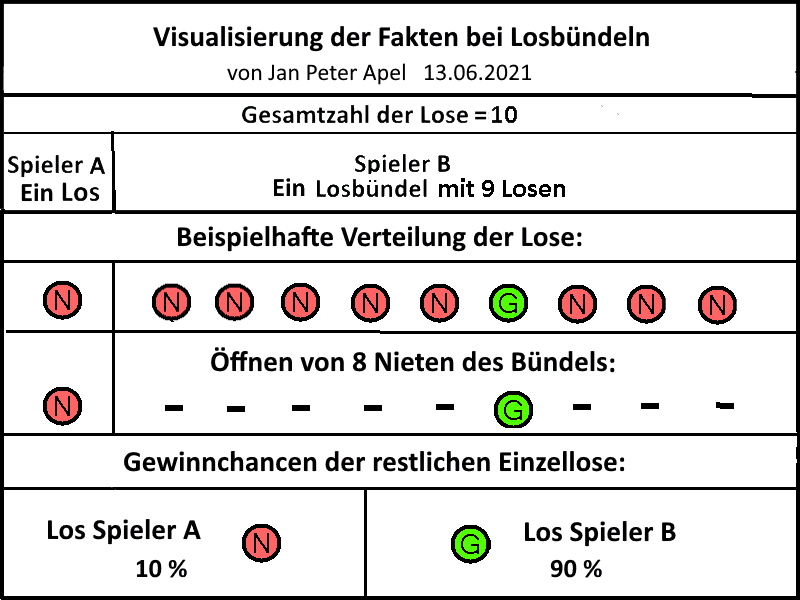
auf sich hat, zeigt die folgende Wahrheitstabelle.
Da ein Gewinnlos bei der Verteilung der Lose statistisch zu 90
Prozent ins Bündel des Spielers B gerät, erhält dieser zwangsläufig
eine 90prozentige Gewinnchance, die erstaunlicherweise auch noch nach
Aussondern von 8 Nieten aus seinem Bündel durch dessen letztem Los
repräsentiert wird.
Die zwei übrig gebliebenen Lose stehen sich nun nicht mehr als
gleichwertig gegenüber, denn das Los aus dem Bündel trägt dessen
Gesamtgewinnchance noch in sich. Die Gesamtchance eines Los-Bündels ist
also nicht auf dessen Einzellose
zuordbar. Je mehr Nieten aus dem Bündel aufgedeckt werden,
um so höher werden die Einzel-Chancen der übrig gebliebenen.
Daraus ergibt sich nun eine weitere
Regel für die Wahrscheinlichkeitslehre:
Regel 2: Ein
letztes Los aus einem Losbündel hat immer noch
die
Gewinnwahrscheinlichkeit des gesamten Bündels!
Das ist eine Regel für die Wahrscheinlichkeitstheorie bei
Losspielen, die niemals mathematisch hätte gefunden werden
können.
Beim Ziegenspiel hat das
Bündel des Moderators von zwei Losen eine Gewinnquote von zwei
Drittel. Wechselt also der Ratekandidat von seiner erstgewählten Tür
mit ein Drittel Gewinnchance zur letzten Tür des Bündels des
Moderators, erhält er, da es dessen letztes Los seines Bündels ist,
auch dessen gesamte Bündelgewinnquote von zwei Drittel, so, wie es die
Wahrheitstabellen und die Realität des Spiels auch zeigen.
Die richtige Denke des Ratekandidaten mit der
Kenntnis dieser Regeln für Losspiele ist also:
"Ich habe mit meinem einen Los eine Chance von ein Drittel. Der
Moderator
hat mit seinem Losbündel von zwei Losen eine Chance von zwei Dritteln.
Wenn der mir verrät, welches seiner zwei Lose eine Niete ist, hat
sein letztes Los allein immer noch die zwei Drittel Chance des
gesamten Losbündels, das Auto zu gewinnen, also tausche ich".
Durch die Tatsache, daß Lose in einem Losbündel keine diskrete
eigenständige
Wertigkeit besitzen, ergibt sich eine dritte Regel:
Regel 3: Es
muß grundsätzlich in Losbündeln gedacht werden und nicht in
Einzellosen.
Beim Ziegenspiel besteht nach der Erstwahl des Ratekandidaten eine
Losverteilung von einem Los für den Kandidaten und einem Losbündel mit
zwei Losen für den Moderator. Damit sind für die Gewinnchancen der
Teilnehmer die Würfel gefallen. Durch die Öffnung einer Niete aus dem
Los-Bündel
des Moderators erhält dessen zweites Los eine alleinige
Gewinnchancenwertigkeit von zwei Drittel.
Aus
der Wahrheitstabelle der Visualisierung von Losbündeln ist heraus zu
lesen:
Regel 4: Gewinnquoten
bei Losspielen legen sich bei der Verteilung
der Lose fest.
Das ist die Hauptregel, wenn es um Losspiele geht und geht allen
anderen Überlegungen voran. Die Gewinnchancen von Losen sind nach der
Verteilung nicht mehr beeinflußbar, außer mit Tauschaktionen wie
zuvor. In welcher Reihenfolge oder beim Ziegenspiel
mit welchem Brimborium die Lose geöffnet werden, hat
also keinerlei Auswirkungen mehr auf die Ergebnisse, denn die sind
durch die Verteilung bestimmt.
Das
spezielle Gesamtergebnis
Die Verteilung von Losen führt, üblicherweise durch Verkauf,
zu Einzellosen und kompakt zu betrachtenden Losbündeln.
1) Einzellose haben eine Gewinnquote von eins durch die Gesamtzahl
aller Lose.
2) Losbündel haben eine Gewinnquote in Höhe der Anzahl ihrer
Lose dividiert durch die Gesamtzahl aller Lose.
Damit sind die Gewinnquoten von Einzellosen und Losbündeln bei
Losspielen endgültig festgelegt und unveränderbar. Und natürlich hat
die Gewinnquote für die Summe aller Lose eines Losspiels, also der
Einzellose plus der Losbündel, zusammen den Wert Eins, also 100%.
Eine Besonderheit innerhalb von Losbündeln ist:
Einzellose in Losbündeln haben keine diskreten
Einzelgewinnchancen, sondern deren Gewinnquoten steigen bei Öffnungen
von Nieten aus dem Bündel dadurch, daß sich die
unveränderbare Gesamtgewinnquote des Bündels
auf weniger Lose verteilt. Das letzte Los
eines Losbündels erreicht dann sogar die Gewinnchance des gesamten
Losbündels, nachdem im Bündel bis dahin nur Nieten aufgedeckt
wurden.
Das
qualitative Gesamtergebnis
Grundlage
aller Regeln für Losspiele sind Wahrheitsdiagramme. Davor muß auch
die Mathematik kuschen, Wahrheiten und die Natur sind Bosse,
nicht die Mathematik, sie ist immer nur Slave! Deswegen steht ihr zu
Recht auch kein Nobelpreis zu. Die Lösung des nun mehr als
50 Jahre alten Ziegenrätsels ist ausschließlich durch die Anwendung der
vier
zuvor genannten verbalen
neuen Regeln der Wahrscheinlichkeitslehre erfolgt.
Die zuvor benannten 4 Regeln für Losspiele sind ein Anfang für
das, was einmal wahre Wahrscheinlichkeitslehre werden kann. Wahrscheinlichkeitslehre
ist kein mathematischer
"Ableger", sondern ein eigenständiges Sachgebiet, also eine eigene
Wissenschaft, die nicht der Mathematik zugehörig sein kann, denn:
Sachliche Regeln bestimmen die Lösungen, nicht
mathematische. Das
Auswechseln von
algebraischen Variablen durch physikalische Größen macht aus Mathematik
weder Physik noch mit
Wahrscheinlichkeitsvariablen Wahrscheinlichkeitslehre.
Bilanz
des Ganzen
Das
Wissen der Menschheit besteht nicht aus quantitativ stimmigen
Resultaten, sondern aus verbal und verständlich nachvollziehbaren
Erklärungen, also Regeln oder
Theorien. Mathematik könnte das Ziegenrätsel nie lösen, andernfalls
hätte sie es nach 50 Jahren auch getan. Mathematik ist nur
eine Zahlenwissenschaft und keine Sachwissenschaft. Sachgebiete lassen
sich nur mit den ihnen eigenen verbalen Regeln beherrschen, nicht aber
mit mathematischen: Mathematik kann nicht denken, obwohl in der
Mathematik auch gedacht werden muß, aber nur über ihre
Zahlenhandhabungen. Mathematik kann als Selbstzweck leben,
sucht aber lieber Vorgänge in der Welt, in die sie sich einbringen kann
und seit langem auch mit ihren Regeln dominieren will, obwohl alle
Vorgänge der Welt ihre eigenen sach- oder naturbezogenen Regeln
besitzen, die ganz anderer Art sind und von denen die Mathematik
überhaupt keine Ahnung haben kann. Mathematik kann nur
quantifizierbares Äußeres, also nur Symptome, beschreiben, deren sie
entstehen
lassenden inneren Funktionismen aber niemals
aufdecken oder gar erklären. Nur Erklärungen aber sind das Wissen der
Menschheit.
WIKIPEDIA
als seriöse Enzyklopädie zu bezeichnen, ist mehr als nur fahrlässig.
Ihre Qualität beruht nicht auf Erkenntnissen von Wahrheiten, sondern
nur auf der Qualität anonymer, meist dem Mainstream
folgenden und überwiegend Schullehre-Gläubigen ohne Verantwortung und
unabhängiger Kontrolle.
Wissenschaft
ist die Suche nach Wahrheiten, nicht die Findung mathematischer Formeln!